Sum Root to Leaf Numbers
Difficulty: Medium
Topics: Tree, Depth-First Search, Binary Tree
You are given the root of a binary tree containing digits from 0 to 9 only.
Each root-to-leaf path in the tree represents a number.
- For example, the root-to-leaf path
1 -> 2 -> 3represents the number123.
Return the total sum of all root-to-leaf numbers. Test cases are generated so that the answer will fit in a 32-bit integer.
A leaf node is a node with no children.
Example 1:
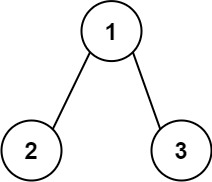
- Input:
<code>root = [1,2,3] - Output:
<code>25 - Explanation:
<code>The root-to-leaf path 1->2 represents the number 12.<code>The root-to-leaf path 1->3 represents the number 13.<code>Therefore, sum = 12 + 13 = 25.
Example 2:
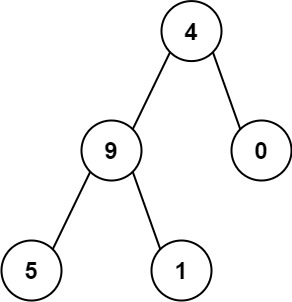
- Input:
<code>root = [4,9,0,5,1] - Output:
<code>1026 - Explanation:
<code>The root-to-leaf path 4->9->5 represents the number 495.<code>The root-to-leaf path 4->9->1 represents the number 491.<code>The root-to-leaf path 4->0 represents the number 40.<code>Therefore, sum = 495 + 491 + 40 = 1026.
Constraints:
- The number of nodes in the tree is in the range
[1, 1000]. 0 <= Node.val <= 9- The depth of the tree will not exceed
10.
Solution:
We can use a Depth-First Search (DFS) approach. The idea is to traverse the tree, keeping track of the number formed by the path from the root to the current node. When you reach a leaf node, you add the current number to the total sum.
Let’s implement this solution in PHP: 129. Sum Root to Leaf Numbers
Table of Contents
Toggle<?php
// Example usage:
// Example 1
$root1 = new TreeNode(1);
$root1->left = new TreeNode(2);
$root1->right = new TreeNode(3);
echo sumNumbers($root1); // Output: 25
// Example 2
$root2 = new TreeNode(4);
$root2->left = new TreeNode(9);
$root2->right = new TreeNode(0);
$root2->left->left = new TreeNode(5);
$root2->left->right = new TreeNode(1);
echo sumNumbers($root2); // Output: 1026
?>Explanation:
- TreeNode Class: This class represents each node of the binary tree. Each node has a value (
val), a left child (left), and a right child (right). - sumNumbers Function: This is the main function that initiates the DFS traversal by calling the
sumNumbersRecufunction with the root node and an initialcurrentSumof 0. - sumNumbersRecu Function:
- Base Case: If the node is
null, return 0 (this handles the case where there is no child node). - Update Current Sum: For each node, update the
currentSumby multiplying the previouscurrentSumby 10 and adding the node’s value. - Leaf Node Check: If the node is a leaf (i.e., it has no left or right child), return the
currentSumas this represents the number formed by the path from the root to this leaf. - Recursive Calls: If the node is not a leaf, recursively call
sumNumbersRecuon both the left and right children and return their sum.
- Base Case: If the node is
Edge Cases:
- The function handles cases where the tree has only one node.
- It correctly computes the sum even for deeper trees, as the depth of the tree will not exceed 10 (as per the problem constraints).
This solution runs efficiently with a time complexity of O(n), where n is the number of nodes in the tree. This is because each node is visited exactly once. The space complexity is O(h), where h is the height of the tree, due to the recursion stack.
Contact Links
If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks 😍. Your support would mean a lot to me!
If you want more helpful content like this, feel free to follow me:
Read More



