4. Median of Two Sorted Arrays

Median of Two Sorted Arrays Solutions:

Difficulty: Hard

Given two sorted arrays nums1 and nums2 of size m and n respectively, return the median of the two sorted arrays.

The overall run time complexity should be O(log (m+n)).

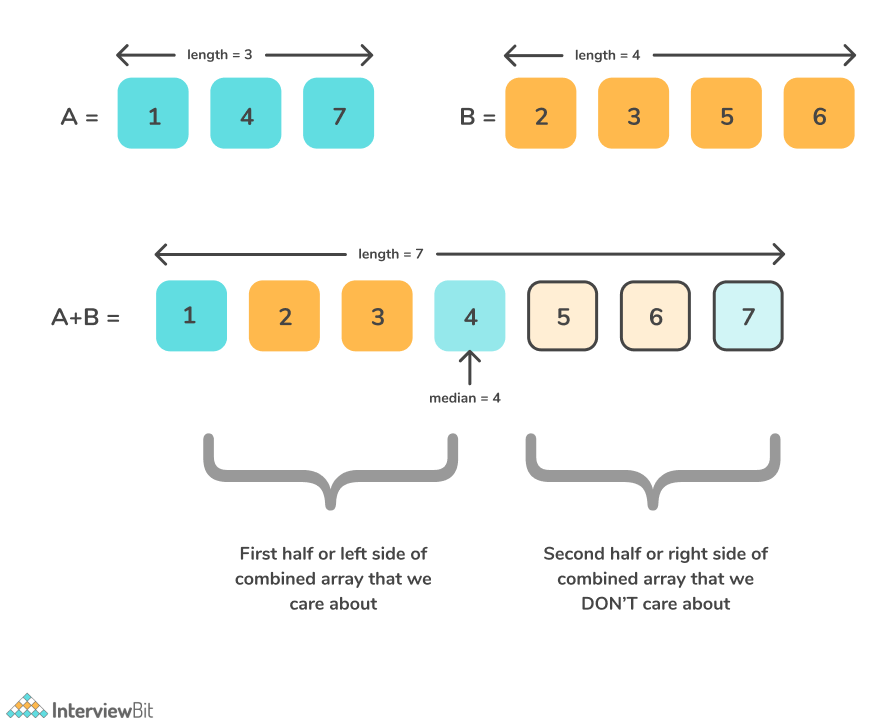
Example 1:

• Input: nums1 = [1,3], nums2 = [2]
• Output: 2.00000
• Explanation: merged array = [1,2,3] and median is 2.

Example 2:

• Input: nums1 = [1,2], nums2 = [3,4]
• Output: 2.50000
• Explanation: merged array = [1,2,3,4] and median is (2 + 3) / 2 = 2.5.

Example 3:

• Input: nums1 = [0,0], nums2 = [0,0]
• Output: 0.00000

Example 4:

• Input: nums1 = [], nums2 = [1]
• Output: 1.00000

Example 5:

• Input: nums1 = [2], nums2 = []
• Output: 2.00000

Constraints:

• nums1.length == m
• nums2.length == n
• 0 <= m <= 1000
• 0 <= n <= 1000
• 1 <= m + n <= 2000
• <code>-10⁶<code> <= nums1[i], nums2[i] <= 10⁶

Solution:

To solve this problem, we can follow these steps:

Let’s implement this solution in PHP: 4. Median of Two Sorted Arrays

<?php
// Example usage:
$nums1 = [1, 3];
$nums2 = [2];
echo findMedianSortedArrays($nums1, $nums2) . "n"; // Output: 2.00000

$nums1 = [1, 2];
$nums2 = [3, 4];
echo findMedianSortedArrays($nums1, $nums2) . "n"; // Output: 2.50000

$nums1 = [0, 0];
$nums2 = [0, 0];
echo findMedianSortedArrays($nums1, $nums2) . "n"; // Output: 0.00000

$nums1 = [];
$nums2 = [1];
echo findMedianSortedArrays($nums1, $nums2) . "n"; // Output: 1.00000

$nums1 = [2];
$nums2 = [];
echo findMedianSortedArrays($nums1, $nums2) . "n"; // Output: 2.00000
?>

Explanation:

1. Partitioning the Arrays:
   • Ensure that nums1 is the smaller array. This simplifies the binary search since we’re always partitioning the smaller array.
   • Initialize imin, imax, and half_len.
   • Use binary search to partition nums1 and nums2 such that all elements on the left of the partition are less than or equal to all elements on the right of the partition.
2. Checking Partitions:
   • Adjust the binary search range based on comparisons between the elements around the partitions.
   • If the partitions are correctly placed, calculate the median based on the maximum elements on the left side and the minimum elements on the right side.
3. Returning the Median:
   • If the total number of elements is odd, the median is the maximum element on the left side.
   • If the total number of elements is even, the median is the average of the maximum element on the left side and the minimum element on the right side.

This solution ensures that the overall run time complexity is (O(log(m+n))).

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks 😍. Your support would mean a lot to me!

If you want more helpful content like this, feel free to follow me:

• LinkedIn
• GitHub

Read More

• 440. K-th Smallest in Lexicographical Order Leetcode Solution
• 432. All O`one Data Structure Leetcode Solution
• 409. Longest Palindrome Leetcode Solution
• 404. Sum of Left Leaves Leetcode Solution
• 402. Remove K Digits Leetcode Solution